Contents:The following concepts are discussed on this page:-
Lever SystemsConsider a lever as a rigid rod that can be acted on by a force. This force is resisted by a load. There are three basic types of lever systems:
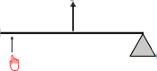
Here the fulcrum is between the effort and the load. 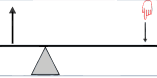
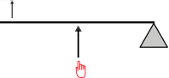
In this lever the fulcrum is a pivot point at he far end of the lever and the effort is applied to the end with the load in the middle.
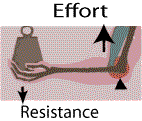 The elbow joint is a class 3 lever system. Here a strong muscle, the biceps acts against the resistance a the hand. The fulcrum is the elbow joint.
The elbow joint is a class 3 lever system. Here a strong muscle, the biceps acts against the resistance a the hand. The fulcrum is the elbow joint.
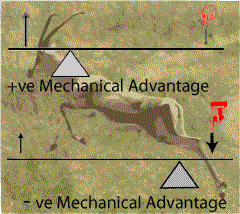
Here, as in many muscular systems the lever system actually works art a mechanical disadvantage. The pull of the muscle is many times it would have to be if it acted nearer the load (at the hand). What is gained by this type of lever system, is speed. Although the muscle has to pull harder, this lever arrangement increases the distance the hand travels a the expense of the force it can
Levers in the skeleton are usually arranged to work at a mechanical disadvantage, and gain speed and distance at the distal side of the lever. RigidityHow rigid a structure is, depends to a large extent, more on it's geometry than on what it is made of.. Rigity depends on: oGeometry of cross section (moment of inertia)
oElasticity of the material (Young’s modulus)
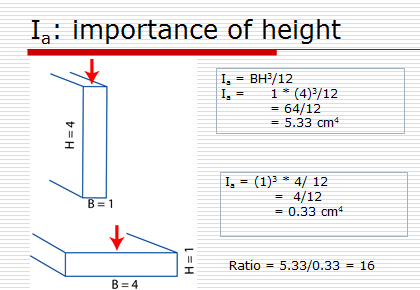
Area moment of inertiaThe area moment of inertia is the resistance to the bending. It depends on the cross sectional geometry of the beam. In the formula the height is cubed. With a rectangular cross section Ia is equal to the height to the power of three times breadth divided by 12. H is the cross sectional dimension in line with the bending force (arrow).
As can be seen in the example above, turning this rectangle on its side decreases its rigidity 16 times. This is because the dim en ti on (H) resisting bending is cubed in the formula for inertia. The way an object is oriented and the height away from the bending point often over ride the influence of elastic modulus of the material itself. Elastic modulusTo understand the elastic modulus of a material, how a material responds to a firce - stress and strain, will have to be understood. Stress
Strain
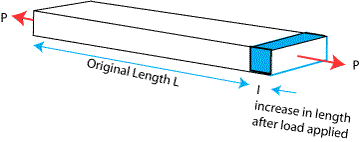 Strain is the increase in length over original length when a stress is applied. Mathematically there are no units, but is often called microstrain or expressed as a percentage of the original length. For example if a 1 meter wire is stretched by 1mm the strain would be 1/1000 = 0.1
Stress Strain Curve
Many materials e.g. metals, remain elastic as they are stressed i. e. they change their length but will return to their original dimensions when the stress is released. Eventually plastic deformity will occur - the material will not be able to return to its original shape, as it has permanently deformed. This is the curved part a the top of the graph. To test a material a test piece is machined to the form of the picture on the right. It is them stretched in an Instong machine and the stress or increasing length is plotted against the pressure (Stress) required. Ultimately the material will fail by snapping giving the ultimate tensile strength (end star on this graph)
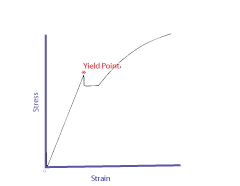
Ductility
Elasticity - Young's Modulus
The elasticity thus determines how much a material will deform. The geometry of the structure is even more important … the moment of inertia can make even an elastic structure rigid if the beam has enough height. Consider an inflatable boat (“rubber duck”) it is made of rubber spaces filled with air, and yet is acceptably rigid! A soft orthopaedic corset works on the same principle.
Bone as a structural material
Cancellous bone is found in the metaphyseal regions. Its function is to spread the load from the joint to the bone shaft. It is therefore more elastic then cotical bone. Cortical bone is seen in the diaphysis and its main function is strength and resisting fracture when loaded. Cancellous bone is 10 to 20% the stiffness of cortical bone. Overloading a joint may lead to a permanent depression in part of the joint surface without evidence of fracture. This is due to the ductility.
Orthopaedic implant materialsFor biological fixation the metal must not corrode, must be non toxic to the body and not only have a high tensile strength, but also have a high fatigue strength. Commonly used materials are stainless steel, cobalt steel and Titanium. Characteristics of implantable materials
Stainless steels are the cheapest implant materials. They are iron with a trace of chrome and other elements. Titanium is the base metal in titanium alloys they are much more elastic than the other two common alloys and this is often an advantage when fracture healing is concerned as it is nearer (although far stiffer than) the elasticity of bone. Cobalt chrome alloys are very strong but more difficult to machine. Stainless steel plates are easier to contour (bend) when fixing fractures as they have a lower yield point and are very ductile.
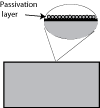
How corrosion can be avoidedSome orthopaedic implant metals (Titanium, Cobalt, Stainless steel) develop a layer of oxide on their surface which is stable.
This layer protects from further corrosion. With stainless steel it is the chrome that develops a tough chrome oxide layer. Deep in the body especially if cracks develop in the implant, the re may be not enough oxygen to form this protective layer. The natural oxide layer is abut 250 Angst oms thick, but can be increased by anodizing. Anoxic conditions in the human body may deprive the metal of oxygen to form this layer. This may occur at the bottom of cracks that may develop in implants over time. This Crevice corrosion can lead to rapid failure of the device.
Sepsis and implant materialsIf an orthopaedic implant becomes septic, it becomes very resistant to treatment by antibiotics.
Micscellaneous biomechanical principlesBiomechanics of gaitUsing a cane
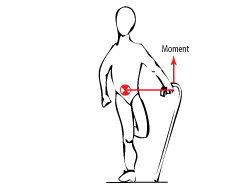
A cane offers pain relief by decreasing load across a joint. It must be used on the opposite side to the painful joint. If the person in the illustration has a painful right hip, a cane used on the left will bring pain relief. The small upward reaction of the ground on this stick will create a long moment arm. This will rotate the pelvis in the same direction the abductor muscles (of the right hip) are acting.. This assistance will lessen the abductor force and thus decrease the force over the hip. This relieves the pain.
Heuter-Volkmann principleThe form of bones is not only determined by genetic factors. Environmental forces also play a major role.Carl Heuter (1870) stated "Compression forces inhibit growth and tensile forces stimulate growth" The practical result of this principle is: The rate of epiphyseal growth is affected by pressures applied to its axes: increased pressure inhibits growth; decreased pressure accelerates growth. The vertebrae of a child with scoliosis will thus grow less on the relatively compressed concave side, making the curve progress. http://pgocclusion.com/files/Stokes.pdf The Heuter Vlokman principle will prove to be a major obstacle to future long distance space flight. If children are on board, they will, because of absent gravity and this law, grow with major deformities!
|
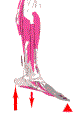
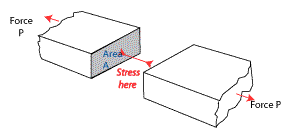 Stress is force per unit area. . SI units are Pascals. Because a Pascal is in Newtons per square meter the values are high typically Mega Pascals (Mpa) for steel, bone or concrete.
Stress is force per unit area. . SI units are Pascals. Because a Pascal is in Newtons per square meter the values are high typically Mega Pascals (Mpa) for steel, bone or concrete.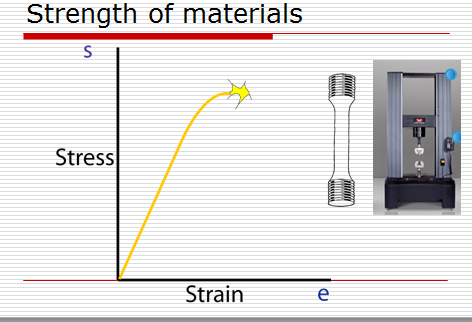
 The
The 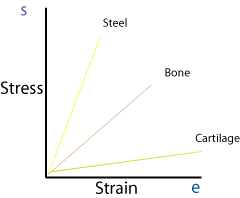 Each material has an elasticity which is constant for that substance. Young’s modulus is defined as stress / strain. Here is the stress /strain graph for some common materials. The modulus of elasticity can be thought of as the slope on a stress strain graph.
Each material has an elasticity which is constant for that substance. Young’s modulus is defined as stress / strain. Here is the stress /strain graph for some common materials. The modulus of elasticity can be thought of as the slope on a stress strain graph.